선분 교차 판정 문제

해당 문제의 기본형 문제입니다. 위 문제를 먼저 푸는 것을 권장합니다.
[문제 풀이]
두 선분이 주어졌을 때 두 선분의 교차 여부와 교점을 찾는 문제입니다.
교차하지 않거나 교차하는 점이 무수히 많다면 교점을 출력하지 않습니다.
우선, 다행히도 한 선분을 이루는 두 점은 겹치지 않습니다.
두 점이 겹쳤다면 문제가 상당히 귀찮아집니다.
선분 교차 2의 풀이에서 더 귀찮아진 형태입니다.
테스트 케이스도 상당히 견고해서 집중하고 코드를 짜야합니다.
설명하기에 앞서, 선분 교차 2를 완벽히 이해했다는 가정 하에 설명하겠습니다.
또한 네 점을 p1, p2, p3, p4라고 하고
CCW(p1, p2, p3) = S1, CCW(p1, p2, p4) = S2, CCW(p3, p4, p1) = S3, CCW(p3, p4, p2) = S4라고 하겠습니다.
우선 선분 교차 2와 달라진 점은 교점을 출력하는 것밖에 없으나, 이게 상당히 복잡해 보입니다.
차분하게 case를 나눠야 하는 요소를 생각해봅시다.
- 교차하는 점이 무수히 많다면 교점을 출력하지 않는다.
- 교점을 구하기 위해서 직선의 방정식을 사용하고, 필연적으로 기울기를 구해야 하는데 기울기가 무한일 수 있다.
이 두 가지 때문에 case를 더 세세하게 나눠줘야 합니다.
물론 기울기 없이 이분 탐색과 ccw를 사용하여 교점을 구할 수도 있지만 시간제한이 0.25초라 시간 초과가 걸리게 됩니다.
case를 나누기에 앞서 선분 교차 2를 풀 때 기본적으로 썼던 if문을 생각해 봅시다.
if (S1 * S2 <= 0 && S3 * S4 < 0 || S1 * S2 < 0 && S3 * S4 <= 0) // 1
else if (S1 * S2 == 0 && S3 * S4 == 0) // 2
else // 3크게 1, 2, 3번처럼 나눌 수 있었습니다.
1번의 경우는 교차하고 2번의 경우는 교차할 수도 있고 3번의 경우만 교차하지 않았습니다.
우선, 3번의 경우는 간단합니다. 선분 교차 2에서 하던 대로 0을 출력합시다.
또한 1번의 경우도 비교적 간단합니다. 무조건 교차하므로 1을 출력하고 교점을 구해줍시다.
다만 위에서 생각한 대로 기울기가 무한인 경우와 아닌 경우를 따로 생각해야 합니다.
기울기가 무한인 경우
x = a형태이므로 교점을 구하는 것은 오히려 더 간단합니다.
기울기가 무한이 아닌 경우
두 직선의 기울기를 구하고, 직선의 방정식을 만들어 연립해줍시다.
다만, 방정식을 코딩으로 표현하기 어려우므로 직접 손으로 연립해준 뒤, x에 대한 식으로 바꿔줍니다.
x를 구했으니 y값은 직선의 방정식에 대입만 하면 구할 수 있습니다.
x에 대해 연립하면 x = (sl1 * p1.x - sl2 * p3.x + p3.y - p1.y) / (sl1 - sl2)라는 식이 나오므로 대입합시다.
(이때 sl1 = p1과 p2의 기울기, sl2는 p3와 p4의 기울기)
문제는 2번의 경우입니다.
2번의 경우는 교점이 무수히 많을 수도 있고, 교점이 한 개일 수도 있고, 교점이 없을 수도 있습니다.
2번의 경우를 그림으로 나눠보면 아래와 같습니다.

위 그림을 왼쪽부터 ㄱ, ㄴ, ㄷ, ㄹ의 경우라고 한다면,
ㄱ, ㄴ, ㄷ은 S1, S2, S3, S4가 전부 0인 경우입니다.
ㄹ만 ccw값들이 모두 0이 아니므로 우선 ㄹ의 경우만 따로 예외처리를 해야 합니다.
선분 교차 2에서는 위의 경우에 대해 예외처리를 하지 않았으나 해당 문제에서는 교점이 무수히 많은 경우를 배제해야 하므로 위의 경우를 나누어야 합니다.
(2023-05-01 수정)
취소선을 그은 부분에 대한 설명이 잘못되어 수정합니다.
두 선분이 한 점에서 만난 게 B, D이든 A, C이든 상관없습니다.
애초에 S1 * S2 == 0 이면서 S3 * S4 == 0인 경우는 한 점에서 만나거나 평행한 경우밖에 없으니 ㄱ, ㄴ, ㄷ처럼 평행한 경우에 대해서 case를 나누고 그 외의 경우는 한 점에서 만났다고 판단하면 됩니다.
여기서 의문점이 들 수 있습니다. ㄷ도 ㄹ도 서로 한 점에서 만난 것인데 왜 ㄹ만 예외 처리를 할까?
이에 대한 자세한 설명을 드리자면 ㄱ, ㄴ, ㄷ처럼 S1, S2, S3, S4가 전부 0인 경우에 교점을 확인하는 방법은
- A < D and C < B : 교점이 무수히 많음 (ㄱ)
- B < C or D < A : 교점이 없음 (ㄴ)
- (A < D and B == C) or (A == D and C < B) : 교점이 한 개 (ㄷ)
처럼 세 가지로 존재합니다.
문제는, ㄹ의 경우에 한 점에서 만나긴 했지만 B, D가 만났다는 것입니다.
ㄷ의 경우는 B == C거나 A == D인데 ㄹ은 B, D가 만났습니다.
아래 그림으로 이것이 왜 문제인지 확인할 수 있을 겁니다.
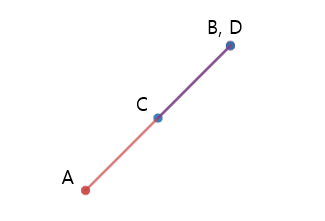
위 그림은 ㄹ과 동일하게 B == D and A < C입니다. 그럼에도 무수히 많은 교점이 생겼습니다.
단순히 B와 D가 같다는 것은 ㄱ의 조건인 A < D and C < B를 만족하게 됩니다.
그러므로 ㄹ과 같은 조건이나 S1, S2, S3, S4가 전부 0이고 ㄱ의 조건을 만족하여 무수히 많은 점이 생기게 되고 ㄹ과는 다른 결과가 나오게 된 것입니다.
다시 본론으로 돌아와서, S1 == 0 and S2 == 0 and S3 == 0 and S4 == 0인지 확인하는 if문을 만들어 ㄱ, ㄴ, ㄷ과 ㄹ을 구분합시다.
ㄹ의 경우에는 무조건 한 점에서 만나는 것이므로 1을 출력하고 교점을 찾아서 출력합시다.
ㄱ, ㄴ, ㄷ의 경우는 위의 교점이 있는지 확인하는 방법을 사용합니다.
ㄱ의 경우에는 교점이 무수히 많으므로 1만 출력합니다.
ㄴ의 경우에는 교점이 없으므로 0을 출력합니다.
ㄷ의 경우에는 한 점에서 만난 것이므로 1을 출력하고 교점을 찾아서 출력합니다.
ㄷ과 ㄹ에서 겹치는 한 점을 찾는 과정은 하드코딩으로 해결했습니다. 더 좋은 방법이 있을 것 같지만 저는 찾지 못했습니다.
이렇게 해서 우리는 1, 2, 3번에 대한 모든 출력을 마쳤습니다.
나눈 케이스를 대충 표현해보면
1 - 기울기 무한 / 직선의 방정식
2 - ㄱ / ㄴ / ㄷ / ㄹ
3
처럼 생각할 수 있겠습니다.
케이스를 나누는 것이 상당히 복잡했지만 차근차근 생각해보면 풀 수 있는 문제였습니다.
[소스 코드] / Java
코드가 상당히 복잡하지만 solve함수에서 if문을 사용하여 case를 나눈 것에 집중하면서 천천히 읽어보시면 이해하기 편할 겁니다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
Point p1 = new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())), p2 = new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
st = new StringTokenizer(br.readLine(), " ");
Point p3 = new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())), p4 = new Point(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
System.out.println(solve(p1, p2, p3, p4));
br.close();
}
private static String solve(Point p1, Point p2, Point p3, Point p4) {
StringBuilder sb = new StringBuilder();
int S1, S2, S3, S4, S12, S34;
S1 = CCW(p1, p2, p3); S2 = CCW(p1, p2, p4); S3 = CCW(p3, p4, p1); S4 = CCW(p3, p4, p2);
S12 = S1 * S2; S34 = S3 * S4;
if (S12 <= 0 && S34 < 0 || S12 < 0 && S34 <= 0) {
sb.append(1).append('\n');
String T1 = getSlope(p1, p2), T2 = getSlope(p3, p4);
double x, y;
if (T1.equals("INF")) {
x = p1.x;
double sl2 = Double.parseDouble(T2);
y = sl2 * (x - p3.x) + p3.y;
} else if (T2.equals("INF")) {
x = p3.x;
double sl1 = Double.parseDouble(T1);
y = sl1 * (x - p1.x) + p1.y;
} else {
double sl1 = Double.parseDouble(T1), sl2 = Double.parseDouble(T2);
x = (sl1 * p1.x - sl2 * p3.x + p3.y - p1.y) / (sl1 - sl2);
y = sl1 * (x - p1.x) + p1.y;
}
sb.append(x).append(' ').append(y);
} else if (S12 == 0 && S34 == 0) {
if (S1 == 0 && S2 == 0 && S3 == 0 && S4 == 0) {
int n = isCrossed(p1, p2, p3, p4);
if (n > 0) sb.append(1);
else sb.append(0);
if (n == 2) {
sb.append('\n');
if (p1.x == p3.x && p1.y == p3.y || p1.x == p4.x && p1.y == p4.y) sb.append(p1.x).append(' ').append(p1.y);
else if (p2.x == p3.x && p2.y == p3.y || p2.x == p4.x && p2.y == p4.y) sb.append(p2.x).append(' ').append(p2.y);
}
}
else {
sb.append(1).append('\n');
if (p1.x == p3.x && p1.y == p3.y || p1.x == p4.x && p1.y == p4.y) sb.append(p1.x).append(' ').append(p1.y);
else if (p2.x == p3.x && p2.y == p3.y || p2.x == p4.x && p2.y == p4.y) sb.append(p2.x).append(' ').append(p2.y);
}
} else sb.append(0);
return sb.toString();
}
private static String getSlope(Point p1, Point p2) {
if (p1.x == p2.x) return "INF";
double s = ((double) p2.y - p1.y) / (p2.x - p1.x);
return String.valueOf(s);
}
private static int isCrossed(Point p1, Point p2, Point p3, Point p4) {
int A, B, C, D;
if (p1.x == p2.x) {
A = Min(p1.y, p2.y); B = Max(p1.y, p2.y);
C = Min(p3.y, p4.y); D = Max(p3.y, p4.y);
} else {
A = Min(p1.x, p2.x); B = Max(p1.x, p2.x);
C = Min(p3.x, p4.x); D = Max(p3.x, p4.x);
}
if (A == D || B == C) return 2;
else if (A < D && C < B) return 1;
else return 0;
}
private static int CCW(Point p1, Point p2, Point p3) {
long S = (long) p1.x * p2.y + (long) p2.x * p3.y + (long) p3.x * p1.y;
S -= (long) p1.y * p2.x + (long) p2.y * p3.x + (long) p3.y * p1.x;
if (S == 0) return 0;
return S > 0 ? 1 : -1;
}
private static int Max(int a, int b) {
return a <= b ? b : a;
}
private static int Min(int a, int b) {
return a <= b ? a : b;
}
private static class Point {
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
}
'Algorithm > BOJ' 카테고리의 다른 글
| [백준 11501] 주식 (0) | 2021.01.25 |
|---|---|
| [백준 20500] Ezreal 여눈부터 가네 ㅈㅈ (0) | 2021.01.24 |
| [백준 2217] 로프 (0) | 2021.01.17 |
| [백준 16975] 수열과 쿼리 21 (0) | 2021.01.08 |
| [백준 2629] 양팔저울 (0) | 2021.01.04 |



