그리디 문제

[문제 풀이]
N개의 주가가 주어졌을 때, 최대 이익을 내는 문제입니다.
N의 제한이 1,000,000입니다. 테스트 케이스까지 존재하므로 무조건 $O(N)$의 시간 복잡도로 해결해야 합니다.
우선 최대 이익을 내는 방법을 생각해보겠습니다.
주식을 계속 사들인 다음에 최대 가치일 때 한 번에 팔아버리면 당연히 최대로 이익을 얻을 수 있습니다.
예를 들어 주가가 1, 5, 10일 때, 1을 사고 굳이 5에 팔기보다, 10에 파는 것이 이득입니다.
즉, 현재 구입하는 시점 이후에서 가장 비쌀 때 팔아버리면 되고 현재 구입하는 시점이 가장 비싸다면 사지 않는 것이 이득입니다.
문제는 현재 구입하는 시점 이후에 가장 비싼 때가 언젠지 모른다는 것입니다.
가장 비싼 때를 찾고 그 이전의 모든 주가에 대한 이익을 계산하면 최악의 경우 $O(N^2)$입니다.
그렇다면 조금 생각을 바꿔보겠습니다.
우리는 계속 주가를 앞에서부터 생각했기 때문에 가장 비싼 때를 찾아야만 했습니다.
하지만 주가를 뒤에서부터 쭉 훑으면서 탐색한다면 어떨까요.
구입하는 시점 이후에서 가장 비쌀 때를 미리 확인하고 사들이는 것입니다.
한 번에 지나가면서 이익도 계산할 수 있고 최댓값도 갱신할 수 있습니다.
앞에서부터 확인하는 방법과 뒤에서부터 확인하는 방법에 무슨 차이가 있는지 그림으로 보여드리겠습니다.
그림에서 주황색으로 칠해진 부분은 현재 보고 있는 주가이고, 파란색으로 칠해진 부분은 이익 계산이 끝난 부분입니다.
그리고 다음과 같은 주가가 주어졌다고 하겠습니다.
6 4 3 7 1 2 5 3 2
우선 앞에서부터 확인하는 방법입니다.






모든 과정마다 현재 범위 내의 최댓값을 구해서 최댓값 이전까지의 모든 주가에 대해 이익을 내는 방법입니다.
문제는 범위가 [7, 8]인 부분을 진행하는 것처럼 현재 진행하는 값이 최댓값인 경우에 의해 $O(N^2)$의 시간 복잡도를 갖게 됩니다.
뒤에서부터 확인하는 방법입니다.

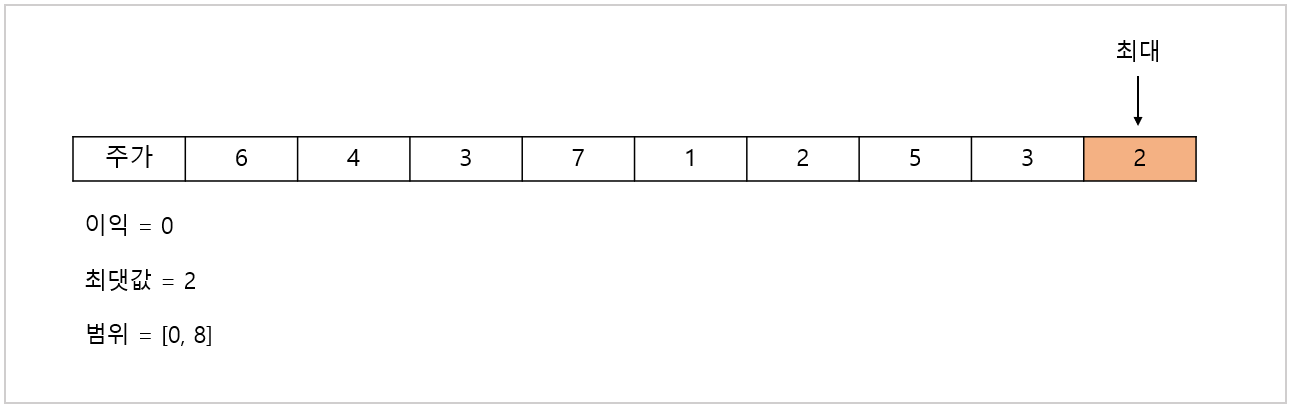









뒤에서부터 한 번에 탐색하면서 최댓값 갱신 및 이익을 계산할 수 있습니다.
현재 저장된 최댓값보다 현재 탐색하는 값이 더 크다면 최댓값을 갱신하고, 그렇지 않다면 이익이 발생하므로 (최댓값) - (현재값)을 계산하여 이익에 더해줍니다.
위와 같은 방법으로 $O(N)$의 시간 복잡도로 해당 문제를 풀이할 수 있습니다.
[소스 코드] / C++
#include <iostream>
#include <vector>
#include <sstream>
using namespace std;
typedef long long ll;
vector<int> price;
ll getMaxProfit(int N) {
ll result = 0;
int j = N - 1;
for (int i = N - 2; i > -1; i--) {
if (price[i] < price[j]) result += price[j] - price[i];
else j = i;
}
return result;
}
int main() {
cin.tie(NULL);
cout.tie(NULL);
ios_base::sync_with_stdio(false);
int T;
cin >> T;
stringstream ss;
while (T--) {
int N;
cin >> N;
price.resize(N);
; for (int i = 0; i < N; i++) {
cin >> price[i];
}
ss << getMaxProfit(N) << '\n';
}
cout << ss.str();
return 0;
}'Algorithm > BOJ' 카테고리의 다른 글
| [백준 7662] 이중 우선순위 큐 (0) | 2021.03.10 |
|---|---|
| [백준 12899] 데이터 구조 (0) | 2021.02.21 |
| [백준 20500] Ezreal 여눈부터 가네 ㅈㅈ (0) | 2021.01.24 |
| [백준 20149] 선분 교차 3 (0) | 2021.01.21 |
| [백준 2217] 로프 (0) | 2021.01.17 |



